“Deus, o arquiteto do universo”, iluminura em pergaminho, elaborada entre 1.220 e 1.230. Para muitos estudiosos medievais, a ciência – e particularmente a geometria e a astronomia – estavam ligados ao divino.
A |
Os pés andando para trás (segundo nosso sentido de escrita e leitura, da esquerda para a direita) indica uma subtração. Neste exemplo, as dezenas e as unidades do minuendo 546, respectivamente 4 e 6, são menores que as dezenas e as unidades do subtraendo 287 (8 e 7). Sempre que ocorrerem situações como esta, o minuendo deve ser ajustado, de modo que sua quantidade de hieróglifos esteja sempre em maior número que a quantidade de hieróglifos do subtraendo. Assim, substituímos 1 rolo de corda por 10 pedaços de corda no minuendo:
De modo análogo, expandimos as unidades, representadas por traços verticais, substituindo um pedaço de corda por 10 traços verticais, conforme a equivalência quantitativa entre esses hieróglifos. O número 546 finalmente passa a conter 4 rolos de corda, 13 pedaços de corda e 16 traços verticais, assumindo a seguinte forma:
Agora que a quantidade de hieróglifos do minuendo (546) são maiores que a correspondente quantidade de hieróglifos do subtraendo (287), a subtração não só é possível, como muito simples. Começando pelos traços verticais, subtraímos 7 traços de 16, restando 9. Obteremos o resultado parcial abaixo:
Cujo valor decimal corresponde a 259, que é o resultado de 546 – 287. Se a soma egípcia não era muito prática, a subtração tampouco tornava o cálculo mais simples. Por outro lado, o método maia de subtrair guarda certa semelhança com o egípcio, mas como faziam uso de poucos símbolos para representar seus números e como seu sistema numérico era posicional, o procedimento de um modo geral é mais simples e visualmente mais fácil de entender. Assim, usando o exemplo anterior, vejamos como se subtrai 287 de 546 no modo maia. Tal como na soma, colocamos as colunas dos números a serem subtraídos lado a lado, posicionando preferencialmente o minuendo à esquerda e o subtraendo à direita. A operação aritmética e o resultado serão executados no minuendo, deixando o subtraendo inalterado.
Na subtração, para as caixas de mesmo nível, um feijão anula outro feijão e um canudo de palha anula outro canudo. E a substituição de um feijão numa caixa de um determinado nível vale dois canudos de palha na caixa do nível imediatamente abaixo. Como as unidades e as dezenas do minuendo são menores que as do subtraendo, o procedimento maia assemelha-se ao egípcio no sentido de que deixaremos cada caixa do minuendo com uma quantidade maior de feijões e canudos que as correspondentes caixas do subtraendo antes de executar a subtração. Seguindo esse raciocínio, na caixa das unidades temos menos feijões no minuendo que no subtraendo. Então, pegaremos um feijão da caixa das dezenas no minuendo e o transformaremos em dois canudos de palha na caixa das unidades; ao mesmo tempo, um destes canudos será convertido em 5 feijões. O resultado parcial será:
Na caixa das dezenas, o minuendo possui igual número de feijões que o subtraendo, mas não tem nenhum canudo. Então, substituímos o canudo das centenas por 5 feijões e passamos um deles para baixo, que será transformado em dois canudos. O novo resultado até aqui será:
Como a caixa das centenas do minuendo tem mais feijões que a do subtraendo, então agora podemos proceder à subtração de fato. Na caixa das unidades, anulamos respectivamente um canudo e dois feijões do minuendo com um canudo e dois feijões do subtraendo, resultando:
Na caixa das dezenas, seguimos o mesmo raciocínio: anulamos um canudo e três feijões do minuendo, em correspondência à mesma quantidade de feijões e canudo na caixa das dezenas do subtraendo; o novo resultado parcial será:
Por fim, na caixa das centenas, anularemos dois feijões do minuendo, em correspondência aos dois feijões do subtraendo. O resultado final será:
O número decorrente da subtração, obtido na coluna à esquerda (onde antes estava o minuendo), como não poderia deixar de ser, é 259. De fato, o método maia de calcular é muito interessante e sem dúvida um dos mais eficientes e eficazes do mundo antigo. Voltando agora nossos olhos para a civilização helênica, vejamos como os gregos procediam à subtração por meio da geometria e, na sequência, através da aritmética. Sendo assim, se gregos fôssemos, subtrairíamos geometricamente do seguinte modo: com uma régua, desenhe um segmento de reta, cujas extremidades tenham seus pontos identificados pelas letras A e D.
Novamente com o compasso, construa um círculo com centro em B e raio de magnitude igual a 2. Chame de C o ponto de intersecção entre o segmento de reta AB e o novo círculo.
Enfim, com uma régua, conecte os pontos A e C. Este segmento de reta (destacado em laranja) é a diferença, ou a subtração, dos raios dos círculos azul e vermelho. Simples como a soma geométrica.
Vejamos agora como proceder à subtração aritmética grega de 546 por 287 utilizando como referência o soroban. Primeiramente, zeramos o ábaco:
Em seguida, posicionamos o número 546 no soroban, deslocando as contas em direção à trave central; ou seja, uma conta azul (que vale 5) na vareta (C), 4 contas laranjas (valendo 1 cada) na vareta (B) e 1 conta azul e 1 conta laranja na haste (A), formando o número desejado, conforme abaixo:
Isto posto, iniciemos a subtração de 278 em 546. Primeiro, subtraímos 2 na vareta (C), incorrendo no afastamento da conta azul da trave central e respectiva aproximação de 3 contas laranjas (3 = 5 – 2). Teremos:
Agora, subtraímos 8 na vareta (B); porém, há apenas 4 contas laranjas disponíveis nessa haste para subtração. Assim como na soma, existem regras específicas para subtrações neste ábaco e da qual faremos uso, que estão descritas na tabela a seguir:
A primeira regra é descartada de imediato, pois foi justamente isso que tentamos fazer (subtrair 8); então a segunda regra diz: "subtrair 10 e somar 2", onde subtrair 10 significa diminuir de 1 na vareta à esquerda, ou seja, na (C), e somar 2 significa somar na própria vareta (B) que, já tendo 4, passa a 6, o que implica em aproximar 1 conta azul e manter 1 conta laranja junto à trave central. O resultado será:
Enfim, subtrairemos 7 de 6 na haste (A); novamente, como há menos contas disponíveis que aquelas a serem retiradas, recorremos mais uma vez à tabela. A primeira regra será logo descartada, pois subtrair 7 é o que gostaríamos de ter feito desde o início; então, vamos à segunda regra, que diz: "subtrair 10 e somar 3", onde subtrair 10 significa retirar 1 da vareta à esquerda (ou seja, a (B)), e somar 3 é feito na própria haste (A), aproximando mais 3 contas laranjas à trave central. Teremos:
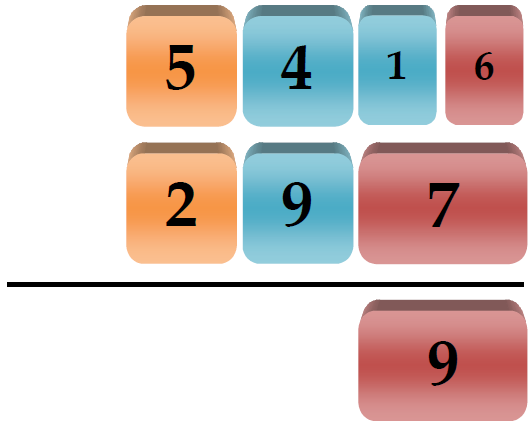
A leitura do ábaco indica o resultado esperado desta subtração: 259. Passando agora para a aritmética hindu, vejamos como esse povo fazia uma subtração, aproveitando o mesmo exemplo usado até aqui: 546 – 287, começando o cálculo da direita para a esquerda (ao contrário do que faziam na soma, onde iniciavam da esquerda para a direita). Havia duas maneiras de calcular. Vejamos a primeira delas:
Neste exemplo, devemos subtrair 7 de 6 nas caixas vermelhas das unidades, mas como 6 é menor que 7, os hindus "pegavam emprestado" no minuendo 1 dezena da caixa azul. Agora é possível subtrair 7 não de 6, mas de 16, restando 9, conforme abaixo:
O próximo passo será diminuir 8 de 3, o que mais uma vez não é possível, exigindo um novo "empréstimo", tomando do minuendo 1 centena na caixa laranja; deste modo, subtraímos 8 não de 3, mas de 13, restando 5, conforme a seguir:
Finalmente, subtraímos 2 de 4, restando 2:
A segunda maneira de subtrair utilizada pelos hindus altera apenas o destinatário dos "empréstimos". Vejamos o mesmo exemplo com esta abordagem: subtrair 7 de 6 exige tomar emprestado 1 dezena, fazendo com que, após o empréstimo, subtraia-se 7 de 16 (como antes) sem, entretanto, alterar o valor das dezenas na caixa azul do minuendo, mas somando uma dezena à caixa azul do subtraendo, conforme mostrado a seguir:
Agora, temos de subtrair 9 de 4, o que mais uma vez não é possível. Então, tomamos emprestado 1 centena, fazendo com que se subtraia 9 de 14 (restando 5), sem alterar o valor das centenas na caixa laranja do minuendo, porém somando 1 centena na caixa laranja do subtraendo, conforme segue:
A conclusão óbvia deste cálculo, subtraindo 3 de 5, restará 2, que é o resultado esperado:
Note que a única coisa que muda nesta abordagem é que, ao invés de subtrair-se o empréstimo uma casa decimal acima, no minuendo, soma-se o empréstimo uma casa decimal acima, no subtraendo. Por fim, na idade média, os matemáticos aprenderam a subtrair com Fibonacci, a partir do quarto capítulo de seu “Liber Abbaci”, cujo método estava assentado na primeira abordagem dos hindus, que é a maneira pela qual aprendemos a subtrair ainda hoje na escola. Agora que já sabemos somar e subtrair segundo o ponto de vista das antigas civilizações, vamos multiplicar nossos conhecimentos!
Referências bibliográficas:
[1] | Fink, K. G. “A brief history of mathematics”, The Open Court Publishing Co., 1900. |
[2] | Cajori, F. “A history of mathematics”, The Macmillan Company, 1909. |
[3] | Cooke, R. L. “The history of mathematics – A brief course”, 3rd Edition, John Willey & Sons, 2013. ISBN: 978-1-118-21756-6. |
[4] | Heath, T. “A history of Greek mathematics – Volume I: From Thales to Euclid”, Oxford at the Calendon Press, 1921. |
[5] | Penrose, R. “The road to reality: A complete guide to the laws of the universe”, Jonathan Cape, 2004. ISBN: 0-224-04447-8. |
[6] | Joseph, G. G. “The crest of the peacock: non-european roots of mathematics”, Princeton University Press, 2011. ISBN: 978-0-691-13526-7. |
[7] | Simmons, G. F. “Calculus Gems: Brief lives and memorable mathematics”, McGraw-Hill Inc., 1992. ISBN: 0-07-057566-5. |
[8] | Sigler, L. “Fibonacci’s Liber Abaci – A translation into modern English of Leonardo Pisano’s Book of Calculation”, Springer Science+Business Media New York, 2003. ISBN: 978-0-387-40737-1; ISBN-e: 978-1-4613-0079-3. |
[9] | Anderson, W. F. “”Arithmetic in Maya numerals”, American Antiquity, Vol. 36, No. 1, 1971. |
[10] | Magaña, L. F. “To learn mathematics: Mayan mathematics in base 10”, Proceedings of EDULEARN 10 Conference, 5th – 7th July 2010, Barcelona, Spain. |
[11] | Høyrup, J. “Leonardo Fibonacci and abbaco culture: a proposal to invert the roles”, Filosofi Og Videnskabsteori På Roskilde Universitetscenter 3. Række: Preprints og reprints, 2004, No. 1. |
[12] | Tejón, F. “Manual para uso do ábaco japonês - Soroban”, Editerio Krayono, Ponferrada, Espanha, 2007. Tradução de Raimundo Viana. |
