|
| Esticadores de corda (à direita) sob supervisão do escriba Djerserkereseneb (ao centro), mensurando uma área para plantio. Tumba do escriba, datada de 1.400 – 1.390 a.C. |
 |
| Plaqueta de argila cozida babilônica, atualmente conhecida pelo código YBC7289 |
Estas inscrições correspondem a agrupamentos de números, como destacado a seguir:
O agrupamento desses glifos gera a seguinte sequência numérica: 1, 24, 51 e 10. Mas, conforme comentado e em função do contexto, esta sequência numérica representa de fato uma soma de frações:
Esta soma de frações equivale à medição da diagonal do quadrado desenhado na plaqueta de argila. Vale dizer que entre 2.900 e 2.300 a.C. a metrologia e a matemática sumérias eram vistas como uma única disciplina, ainda hoje complexa e não totalmente compreendida; todas as quantidades eram escritas como símbolos metrológicos e nunca como numerais seguidos de um símbolo para a unidade mensurada, fosse uma medida de área, de tempo ou de volume, totalizando mais de 600 símbolos diferentes. Entretanto, as medidas de comprimento, volume e massa derivavam de um cubo padrão teórico chamado gur, preenchido com cevada, trigo, água ou óleo. Mas como esses produtos possuem pesos específicos diferentes, os sumérios fizeram uso de vários tamanhos diferentes desses cubos gur, porém sem consenso. Uma grande melhoria nesse sistema de medição surgiria em 2.150 a.C., durante o Império Acadiano, sob o reinado de Naram-Sin, onde os sistemas metrológicos concorrentes foram unificados em um único padrão oficial, o gur-cubo real, um cubóide teórico preenchido com água com medidas aproximadas de 6 metros x 6 metros x 0,5 metro, a partir do qual todas as outras medidas eram derivadas. Assim, para as medidas de comprimento, os povos babilônicos utilizavam as seguintes unidades fracionárias e inteiras:
Comprimento básico | |||
Unidade | Razão | Nome sumério | Nome acadiano |
Grão | 1/180 | še | uţţatu |
Dedo | 1/30 | šu-si | ubānu |
Pé | 2/3 | šu-du | šīzu |
Côvado | 1 | kuš | ammatu |
Passo | 2 | ĝiri | šēpu |
Junco | 6 | kimono | qanû |
Cajado | 12 | nindan | nindanu |
Corda | 120 | eše | aslu |
Já as unidades de distância sumérias eram geodésicas, distintas dos comprimentos básicos, estes não geodésicos:
Distância | |||
Unidade | Razão | Nome sumério | Nome acadiano |
Cajado | 1/60 | nidan | nindanu |
Cordão | 1/6 | eše | aslu |
Cabo | 1 | uš | uš |
Légua | 30 | da-na | bêru |
Para as áreas, os sumérios possuíam uma unidade especial chamada “jardim de tijolos”, que continha 720 tijolos:
Área básica | ||||
Unidade | Razão | Dimensões | Nome sumério | Nome acadiano |
Shekel | 1/60 | 1 kuš × 1 kuš | gin | šiqlu |
Jardim | 1 | 12 kuš × 12 kuš | sar | mūšaru |
Quarto de campo | 5 | 60 kuš × 60 kuš | uzalak | ? |
Meio campo | 10 | 120 kuš × 120 kuš | upu | ubû |
Campo | 100 | 60 ĝiri × 60 ĝiri | iku | ikû |
Estádio | 1800 | 3 eše × 3 eše | bur | būru |
Por outro lado, as capacidades volumétricas eram medidas de acordo com o conteúdo: seco ou úmido; a seguir, as medidas volumétricas fracionárias e inteiras para volumes básicos:
Volume básico | |||
Unidade | Razão | Nome sumério | Nome acadiano |
Shekel | 1/60 | gin | šiqlu |
Tigela | 1 | sila | qû |
Vasilha | 10 | ban | sutū |
Alqueire | 60 | ba-ri-ga | parsiktu |
Gur-cubo | 300 | gur | kurru |
Para massas ou pesos, os valores abaixo são uma média dos artefatos para mensurar pesos nas cidades-estados de Ur e Nippur, representados por ± 1 desvio-padrão, sendo que todos os valores foram arredondados para o segundo dígito do desvio-padrão:
Massa básica | ||||
Unidade | Razão | Valor médio | Nome sumério | Nome acadiano |
Grão | 1/180 | 46,6 ± 1,9 mg | še | uţţatu |
Shekel | 1 | 8,40 ± 0,34 g | gin | šiqlu |
Mina | 60 | 504 ± 20 g | ma-na | manû |
Talento | 3600 | 30,2 ± 1,2 kg | gun | biltu ou kakaru |
Finalmente, para o tempo, existiam vários calendários lunisolares sumérios, porém o calendário civil da cidade de Nippur acabou sendo adotado pela Babilônia como o seu próprio. Este calendário data de 3.500 a.C. e foi baseado em conhecimentos astronômicos ancestrais de origem incerta. Os principais ciclos astronômicos para construir esses calendários eram: o mês sinódico[1] e o dia sideral[2].
Tempo básico | |||
Unidade | Razão | Nome sumério | Nome acadiano |
Gesh | 1/360 | mu-eš | geš |
Vigia | 1/12 | da-na | bêru |
Dia | 1 | ud | immu |
Mês | 30 | itud | arhu |
Ano | 360 | mu | šattu |
[1] Nos calendários lunares, um mês lunar é o tempo entre duas sizígias sucessivas do mesmo tipo: luas novas ou luas cheias. Sizígia: conjunção da lua e do sol, na lua nova e na lua cheia, quando as marés altas são maiores e as marés baixas são menores, que provocam as chamadas marés de águas vivas. (fonte: https://en.wikipedia.org/wiki/Lunar_month#Synodic_month)
[2] Tempo sideral é um sistema de cronometragem que os astrônomos utilizam para localizar objetos celestes. Usando o tempo sideral, é possível apontar facilmente um telescópio para as coordenadas adequadas no céu noturno. Em resumo, o tempo sideral é uma escala de tempo que se baseia na rotação da Terra medida em relação às estrelas fixas. (fonte: https://en.wikipedia.org/wiki/Sidereal_time#Sidereal_day)
 |
| Pesos mesopotâmicos feitos de hematita. O maior pesa 1 mina e o menor 3 shekels |
 |
| Régua-côvado egípcia, atualmente no Museu de Turim |
Além de réguas-côvados, a topografia e a medição eram realizadas pelos egípcios através de cordas com nós:
 |
Pintura na tumba de Menna,construído entre 1.420 e 1411 a.C. no Vale dos Reis. Observe os esticadores de corda mensurando uma terra agricultável |
Nesta cena, podemos observar esticadores de corda sob o comando de Menna (que está segurando o rolo de corda), um oficial com vários títulos associados às propriedades agrícolas do templo de Karnak e do rei egípcio. As unidades de comprimento utilizadas por esta civilização estão descritas a seguir:
Comprimento | |||
Unidade | Razão | Nome egípcio | Valor métrico |
Dedo | 1/4 | db | 1,875 cm |
Palma | 1 | šsp | 7,5 cm |
Mão | 1 ¼ | drt | 9,38 cm |
Punho | 1 ½ | hf | 11,25 cm |
Mão dupla | 2 | šspwy | 15 cm |
Pequeno shat | 3 | p d šsp | 22,5 cm |
Grande shat | 3 ½ | pd | 26 cm |
Braço dobrado | 4 | dsr | 30 cm |
Braço superior | 5 | rmn | 37,5 cm |
Cúbito pequeno | 6 | m h n ds | 45 cm |
Cúbito real | 7 | mh | 52,5 cm |
Nebiu | 8 | nbiw | 60 cm |
Khet | 100 côvados | ht | 52,5 m |
Iteru | 20.000 côvados | itrw | 10,5 km |
Já as unidades de áreas datam desde o início do período dinástico ou arcaico (após a unificação do Alto e do Baixo Egito, por volta de 3.100 a.C.) e registra concessões de terras em termos de kha e setat:
Área | |||
Unidade | Razão | Nome egípcio | Valor métrico |
Sá | 1/800 | z | 3,4456 m2 |
Heseb | 1/400 | hsb | 6,8913 m2 |
Remen | 1/200 | rmn | 13,783 m2 |
Khet | 1/100 | ht | 27,565 m2 |
Kha | 1/10 | h | 275,65 m2 |
Setat | 1 | stt | 2.756,5 m2 |
Unidades de volume aparecem em papiros, como no cálculo do volume de um celeiro circular no problema 42 do papiro de Rhind:
Volume | |||
Unidade | Razão | Nome egípcio | Valor métrico |
Ro | 1/320 | r | 0,015 litro |
Dja | 1/16 | dja | 0,3 litro |
Hinu | 1/10 | hnw | 0,48 litro |
Heqat | 1 | hqt | 4,8 litros |
Duplo heqat | 2 | hqty | 9,6 litros |
Quádruplo heqat | 4 | hqt-fdw | 19,2 litros |
Khar | 16 | khar | 76,8 litros |
Deny | 30 | deny | 144 litros |
 |
| Glifo maia para representação de um período de 10 anos |
[3] Decanos são 36 grupos de estrelas (pequenas constelações) utilizados na antiga astronomia egípcia para dividir convenientemente os 360 graus da elíptica em 36 partes de 10 graus cada. A subida de cada decanato marcava o início de uma nova hora decanal da noite para os antigos egípcios e foram utilizados como relógios estelares siderais pelo menos a partir da 9ª ou 10ª dinastia, cerca de 2.100 a.C.
 |
| Folha do manuscrito Bakhshali, com representação de frações dentro de 'caixas', mas sem o traço característico separando o numerador do denominador |
Os termos sânscritos geralmente aplicados para descrever fração eram: bhinna, cujo significado é “quebrado”, bem como bhaga e amsa, significando “parte” ou “porção”. Na civilização grega, a notação para frações era ambígua e o contexto era de vital importância para a correta leitura de seu valor. Para frações unitárias, por exemplo, os gregos aplicavam a apóstrofe após o denominador; assim: β' equivalia a 1/2 e μβ' era o mesmo que 1/42. Para frações não unitárias, o contexto se mantinha importante, mas nestes casos o numerador era sobrescrito com uma barra e o denominador recebia uma apóstrofe, tudo junto. Desse modo:
 |
| Vaso grego com musa tocando a phorminx, um tipo de lira, 440–430 a.C. |
[4] Segundo Platão, Demiurgo é o artesão divino ou o princípio organizador do universo que, sem criar de fato a realidade, modela e organiza a matéria caótica preexistente através da imitação de modelos eternos e perfeitos.
 |
Exemplo pitagórico de um tetractys |
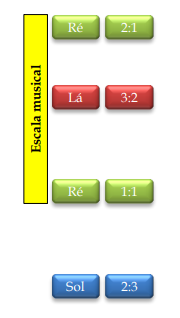
Isto posto, voltemos à questão da lira grega estudada por Pitágoras. Sua primeira observação foi notar que se tivermos duas cordas com o mesmo comprimento, espessura e igualmente tensionadas, elas soarão igualmente quando dedilhadas. Significa dizer que elas possuem o mesmo tom e soam bem (ou consonantes) quando tocadas juntas. A relação, ou intervalo, entre essas notas chama-se uníssono. A segunda observação que Pitágoras fez aponta que, se tivermos duas cordas de comprimentos diferentes, com a mesma espessura e mantido o mesmo tensionamento, as cordas terão tons diferentes que geralmente soarão mal (ou dissonantes) quando dedilhadas em conjunto. Por fim, ele notou que para certos comprimentos as cordas ainda terão diferentes tons, porém soarão consonantes mais que dissonantes. Pitágoras denominou a relação entre essas duas notas de intervalo. Nesta última condição, se uma corda tiver exatamente a metade do comprimento da outra, seu tom será bem maior, mas ainda assim soarão consonantes quando tocadas juntas; este intervalo é denominado oitava. Finalmente, se uma corda tiver exatamente 2/3 do comprimento da outra, elas ainda soarão consonantes quando tocadas juntas e este intervalo é denominado quinta justa. Em resumo, temos as seguintes razões entre as cordas:
Nome | Razão |
Uníssono | 1:1 |
Oitava | 2:1 |
Quinta justa | 3:2 |
Pela combinação desses dois intervalos, produziu-se um terceiro. A este novo intervalo dá-se o nome de quarta justa, definida pela razão 4/3. Em resumo, tem-se que:
ü ü Razões 1/2 e 2/1 geram oitavas
ü ü Razões 2/3 e 3/2 geram quintas justas
ü ü Razões 4/3 e 3/4 geram quartas justas
Partindo do Sol fora da escala, subimos uma oitava, gerando agora um segundo Sol, este dentro da escala. A razão deste segundo Sol é:
Avançando na história, falemos dos romanos, que mesmo com seu intrincado sistema numérico, e sem o número zero, tinham frações! O sistema fracionário romano provinha dos pesos e das medições de terras e era duodecimal, porque a divisibilidade de 12 por 2, 3, 4 e 6 tornava mais fácil o manuseio de frações comuns (como o 1/2, 1/3, 1/4, 1/6, 2/3 e 3/4) que a divisibilidade de 10, que é divisível apenas por 2 e por 5 no sistema decimal. Cada fração romana possuía um nome, conforme a tabela a seguir:
Fração | Numeral Romano | Nome (nominativo e genitivo) | Significado |
1/12 | • | Uncia, unciae | Um doze avos |
2/12 = 1/6 | •• ou : | Sextans, sextantis | Um sexto |
3/12 = 1/4 | ••• ou ∴ | Quadrans, quadrantis | Um quarto |
4/12 = 1/3 | •••• ou :: | Triens, trientis | Um terço |
5/12 | ••••• ou :·: | Quincunx, quincunsis | Cinco doze avos |
6/12 = 1/2 | S | Semis, semissis | Meio |
7/12 | S• | Septunx, septuncis | Sete doze avos |
8/12 = 2/3 | S•• ou S: | Bes, bessis | Dois terços |
9/12 = 3/4 | S••• ou S:· | Dodrans, dodrantis | Menos um quarto |
10/12 = 1/6 | S•••• ou S:: | Dextans | Menos um sexto |
11/12 | S••••• ou S:·: | Deunx | Menos um doze avos |
12/12 = 1 | I | As, assis | Unidade |
 |
Moeda romana triens (4/12 ou 1/3 da unidade), cerca de 241 a 235 a.C. Observe os quatro pontos nas duas faces indicando o seu valor |
A invenção da barra de fração, que divide o numerador do denominador, é atribuída ao matemático árabe Abu Bakr Muhammad ibn Abdallah ibn Ayyash al-Hassar, que viveu no Marrocos no século 12 d.C. Al-Hassar escreveu dois livros: o Kitab al-bayan wat-tadhkar (Livro da demonstração e memorização), um manual de cálculo, e o Kitab al-kamil fi sinaat al-adad (Livro completo na arte dos números) sobre a repartição de números, dividido em duas partes, das quais apenas parte da segunda sobreviveu aos nossos dias, livro este que faz uso das barras para indicar frações. A palavra árabe para fração era alkasr, que vem do verbo “quebrar”. Na idade média é Fibonacci quem primeiro se aproveita das barras de frações, ao demonstrá-las em seu Liber Abaci, como fazemos atualmente, seguindo a prática adotada pelos árabes. Entretanto, a barra horizontal normalmente era omitida nos livros medievais, principalmente após a introdução da prensa de tipos móveis de Gutenberg, talvez devido a dificuldades tipográficas, o que motivou o uso da barra diagonal (/) nas obras da época para a representação de frações simples na mesma linha do texto, um procedimento que adotamos até hoje. Seguindo os rumos da história, é interessante notar que a teoria musical pitagórica foi retomada durante o Renascentismo europeu pelas mãos do teórico musical e compositor italiano Franchino Gaffurio (1.451 – 1.522) – contemporâneo de ninguém menos que Leonardo da Vinci, de quem era amigo pessoal – em sua obra Theorica Musicae, de 1.492.
 |
“Retrato de um Músico” (1.485 a 1.490), óleo sobre tela, por Leonardo da Vinci. Trata-se, possivelmente, de Franchinus Gaffurius |
 |
| Gioseffo Zarlino |
A intenção desta xilogravura é ilustrar as razões pitagóricas e como elas são aplicadas aos instrumentos musicais. O cartão inferior direito mostra flautas cujos comprimentos correspondem a razões pitagóricas. O problema identificado por Vincenzo está no cartão inferior esquerdo: as maças com diferentes pesos penduradas às cordas alteram a tensão aplicada às mesmas; porém, as notas produzidas pelas cordas não estão relacionadas apenas ao tensionamento a elas aplicado, de modo que essas cordas não soarão de acordo com os intervalos pitagóricos. Os exemplos indicados nos cartões superiores da xilogravura são ainda mais complicados, mas é possível dizer que os sinos, os copos d’água e as bigornas tampouco produzirão os intervalos corretos... Fato é que o termo pitagórico “música universal” (representada pelos quatro primeiros números inteiros) ou “música das estrelas” possui conexões históricas entre música, matemática e astronomia, e tiveram um forte impacto nessas disciplinas. Senão, vejamos: os astrônomos gregos postulavam que haviam certas estrelas fixas cujas posições relativas na abóbada celeste não se modificavam ao longo do ano; e também que existiam estrelas errantes que se moviam em relação às estrelas fixas, aos quais davam o nome de planetas (planeta é a palavra grega para errante). Para explicar essas observações, os gregos conceberam uma grande esfera negra que definia os limites do universo, à qual as estrelas fixas estavam apensas. Os planetas ficariam fixos em diversas esferas girantes, umas dentro das outras, internas à esfera negra, tendo a Terra como centro de todas elas (modelo geocêntrico grego); porém, essas esferas internas não poderiam ser igualmente negras, já que ocultariam a esfera-limite do universo bem como ocultar-se-iam umas às outras.
 |
| Modelo grego geocêntrico de esferas para estrelas fixas e errantes |
[5] Como professor de matemática da universidade de Tübingen de 1.583 até 1.631, Kepler estudou tanto o sistema ptolomaico quanto o sistema copernicano dos movimentos planetários, vindo a abraçar este último. Em um debate estudantil, defenderia o heliocentrismo de uma perspectiva tanto teórica quanto teológica, sustentando que o Sol era a principal fonte de poder motriz no Universo.
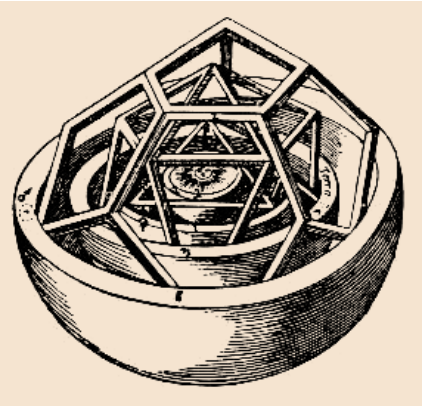 |
Modelo do sistema solar baseado em sólidos platônicos, de Kepler |
Nicolau Copérnico (1.473 a 1.543), astrônomo e matemático polonês, em sua obra De revolutionibus orbium coelestium, de 1.543, cita Pitágoras como sua mais importante influência no desenvolvimento de seu modelo heliocêntrico do universo. Até mesmo o grande matemático e físico inglês Isaac Newton, que sabidamente não era afeito a reconhecer o mérito científico de seus antecessores, via na música pitagórica das esferas uma descrição prévia de sua própria lei da gravitação universal. Um visitante escreveria que:
O Sr. Newton crê, sem sombra de dúvida, que os antigos – tais como Pitágoras, Platão etc. – possuíam todas as demonstrações de que ele mesmo forneceu acerca do verdadeiro sistema do mundo.
Referências bibliográficas:
[1] | Monnier, Fr.; Petit, J. P.; Tardy, Chr., “The use of the ‘ceremonial’ cubit rod as a measuring tool. An explanation”, The Journal of Ancient Egyptian Architecture, Vol. 1, 2016. |
[2] | Zapassky, E.; Gadot, Y.; Finkelstein, I.; Benenson, I., “An Ancient Relation between Units of Length and Volume Based on a Sphere”, PLoS ONE, Volume 7, Issue 3, March 2012. |
[3] | Wikipedia, “Cubit (côvado)”, acessado em Julho/2021. Site: https://en.wikipedia.org/wiki/Cubit#Ancient_Mesopotamian_units_of_measurement |
[4] | Wikipedia, "Ancient Egyptian units of measurement", acessado em Julho/2021. Site: https://en.wikipedia.org/wiki/Ancient_Egyptian_units_of_measurement |
[5] | Hafford, W. B., ”Mesopotamian Mensuration: Balance Pan Weights from Nippur”, Journal of the Economic and Social History of the Orient, 48, 3, 2005. https://www.academia.edu/2916303/Mesopotamian_Mensuration_Balance_Pan_Weights_from_Nippur (acessado em Agosto/2021) |
[6] | Hafford, W. B., “Weighting in Mesopotamia: The Balance Pan Weights from Ur”, Akkadica 133, fasc. 1, 2012. https://www.academia.edu/2916278/Weighing_in_Mesopotamia_The_Balance_Pan_Weights_from_Ur (acessado em Agosto/2021) |
[7] | Wikipedia, “Ancient Mesopotamian units of measurement” (Agosto/2021) https://en.wikipedia.org/wiki/Ancient_Mesopotamian_units_of_measurement |
[8] | Makeig, S.; “Means, meaning and music: Pythagoras, Archytas and Plato”, ex Tempore, Volume 1, 1981. |
[9] | Gibson, G. N.; “The Physics of Music”, Physics 1075Q Course, College of Liberal Arts and Sciences, University of Connecticut. Acessado em Agosto/2021. https://www.phys.uconn.edu/~gibson/courses.html |
[10] | Cartwright, J. H. E.; González, D. L.; Piro, O.; “Dynamical systems, celestial mechanics, and music: Pythagoras revisited”, The Mathematical Intelligencer, volume 43, pp 25–39 (2021) |
[11] | Maher D. W.; Makowski J. F.; "Literary Evidence for Roman Arithmetic with Fractions", Classical Philology 96, 2001, pp 376–399. |
[12] | Collins D. C.; "Continued fractions", MIT undergraduate journal of mathematics, pp 11-18. |
[13] | Sykorova, I.; "Fractions in ancient Indian mathematics", WDS'10 Proceedings of Contributed Papers, Part I, 2010, pp 133–138. |
[14] | Kosheleva O.; Kreinovich V.; "Egyptian fractions revisited", Informatics in Education, 2009, Vol. 8, No. 1, pp 35–48. |